Keras WTTE-RNN and Noisy signals

I was really happy to find daynebatten’s post about implementing WTTE-RNN in keras. Since then I’ve done some work to fully cram WTTE-RNN into Keras and get it up and running. Some things becomes outright hacky (like target has to be the same shape as predicted) but Keras is also a really nice place to mock upp networks and tests and get work done.

If you haven’t checked out the updated Github-project, here’s a quick taste.

Evenly spaced points revisited

I like this example. We know the truth and can modify the signal. The problem is to predict the Time To Event (TTE, black) only knowing what happened up until where you’re predicting from. An added problem is that you can only train on what you have data for (the whole timewindow), leading to censoring (in red). Here looping through the sequences that are possible:

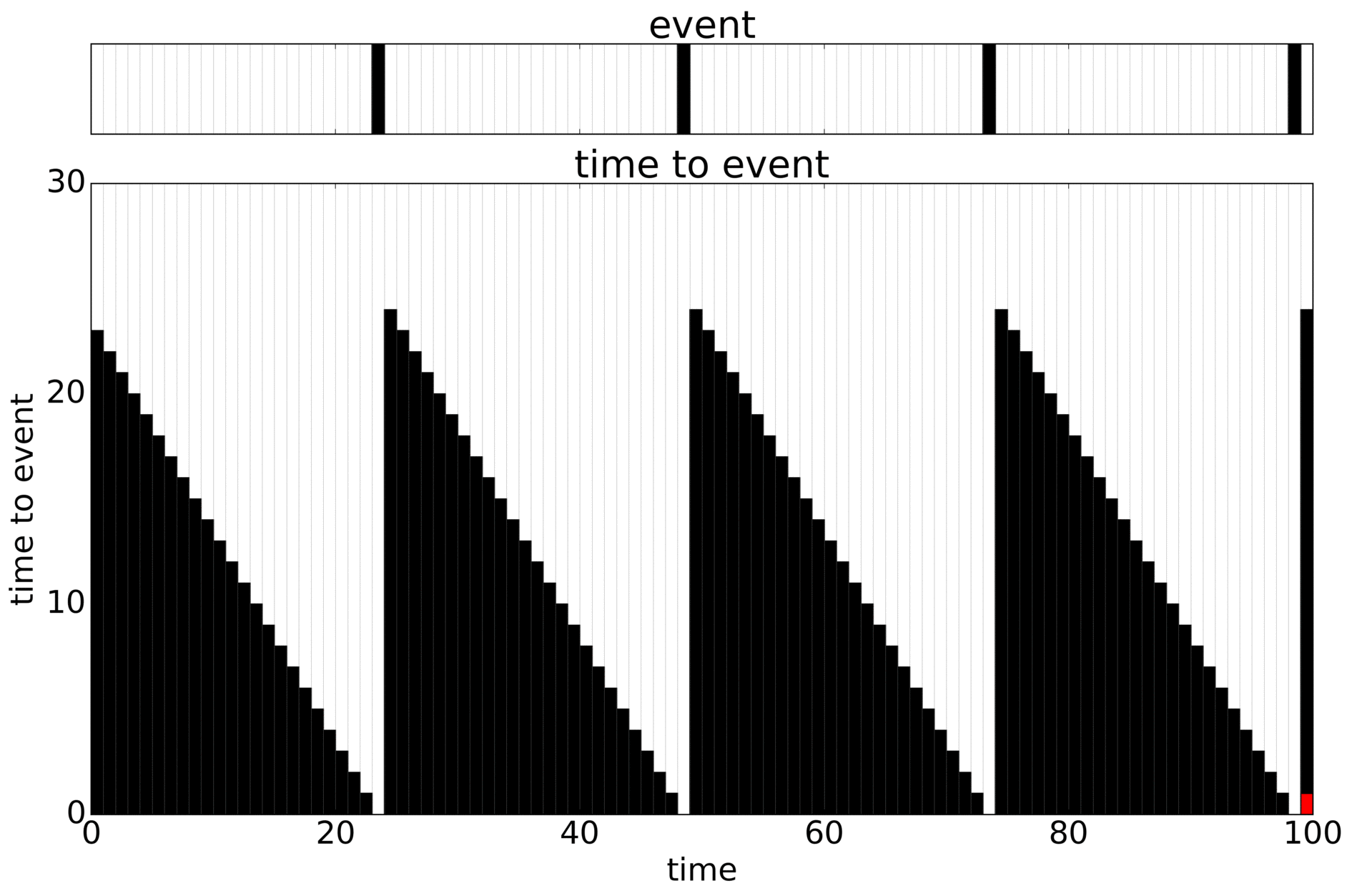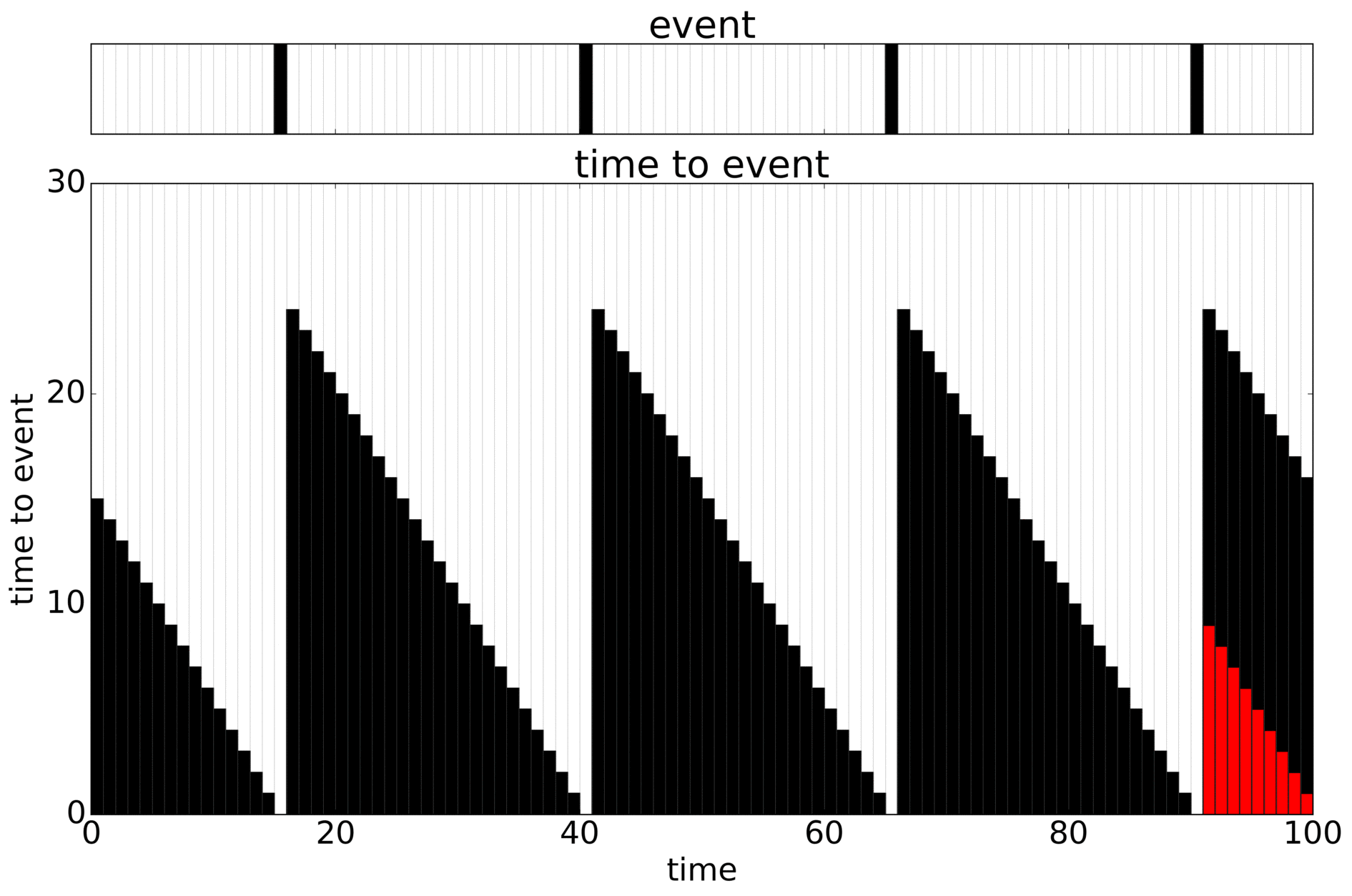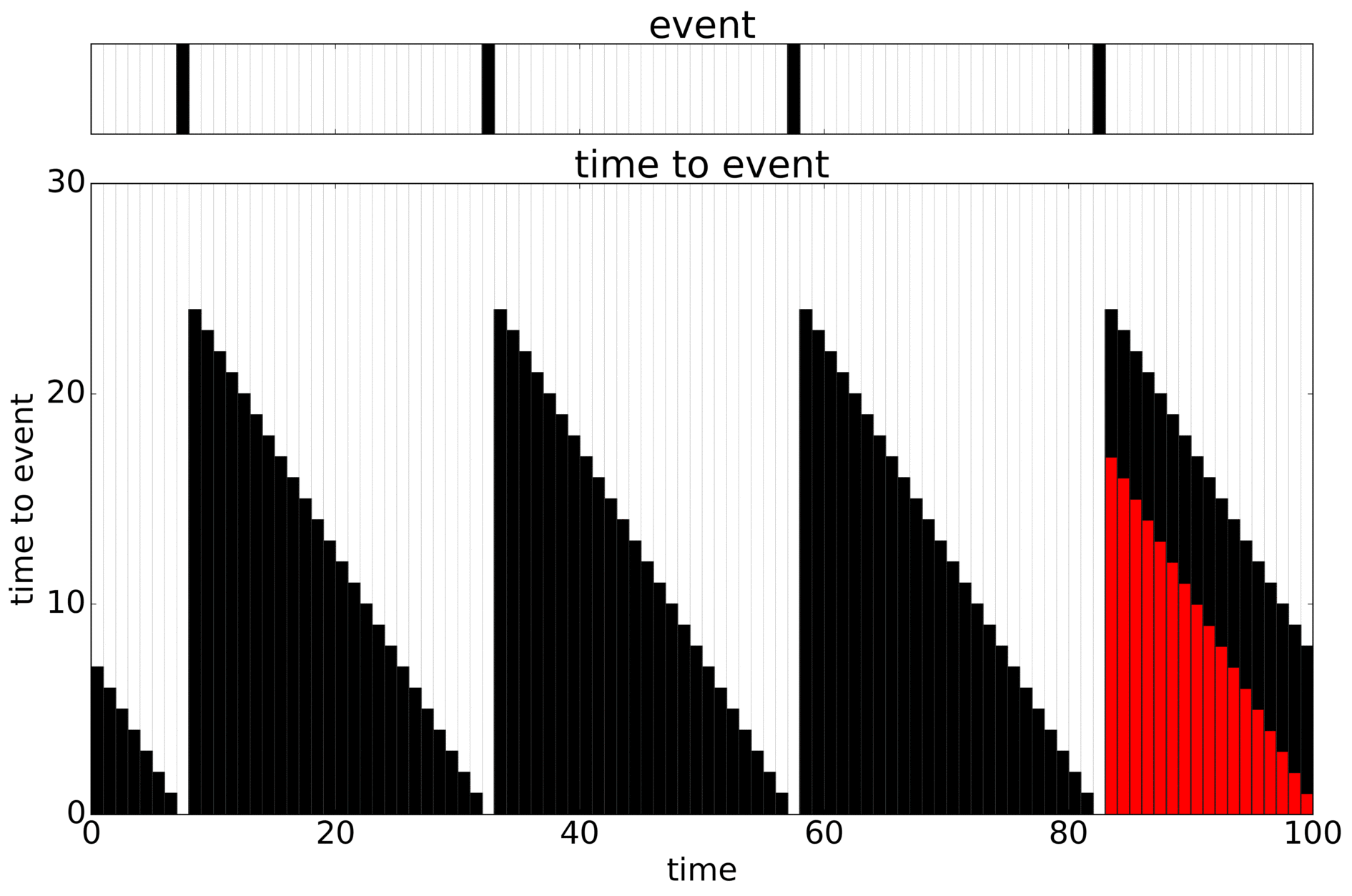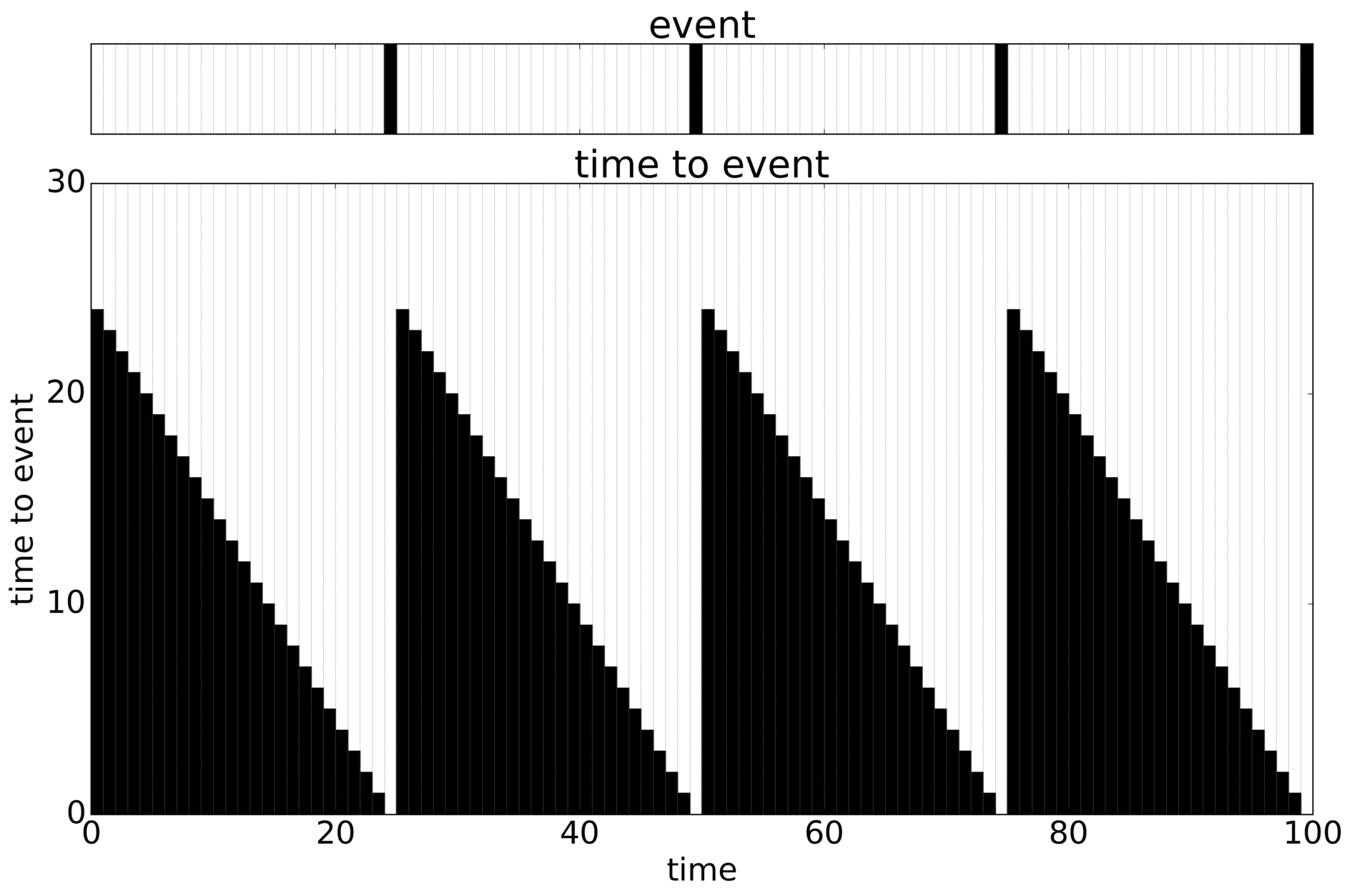
Add some noise

Lets set up a 200-step RNN. As input to the network feed if there was an event in the last step. You use this to predict the number of steps to the next event.

Imagine now that this signal is corrupted by noise. Stacking 160 such sequences on top of eachother looks something like this:

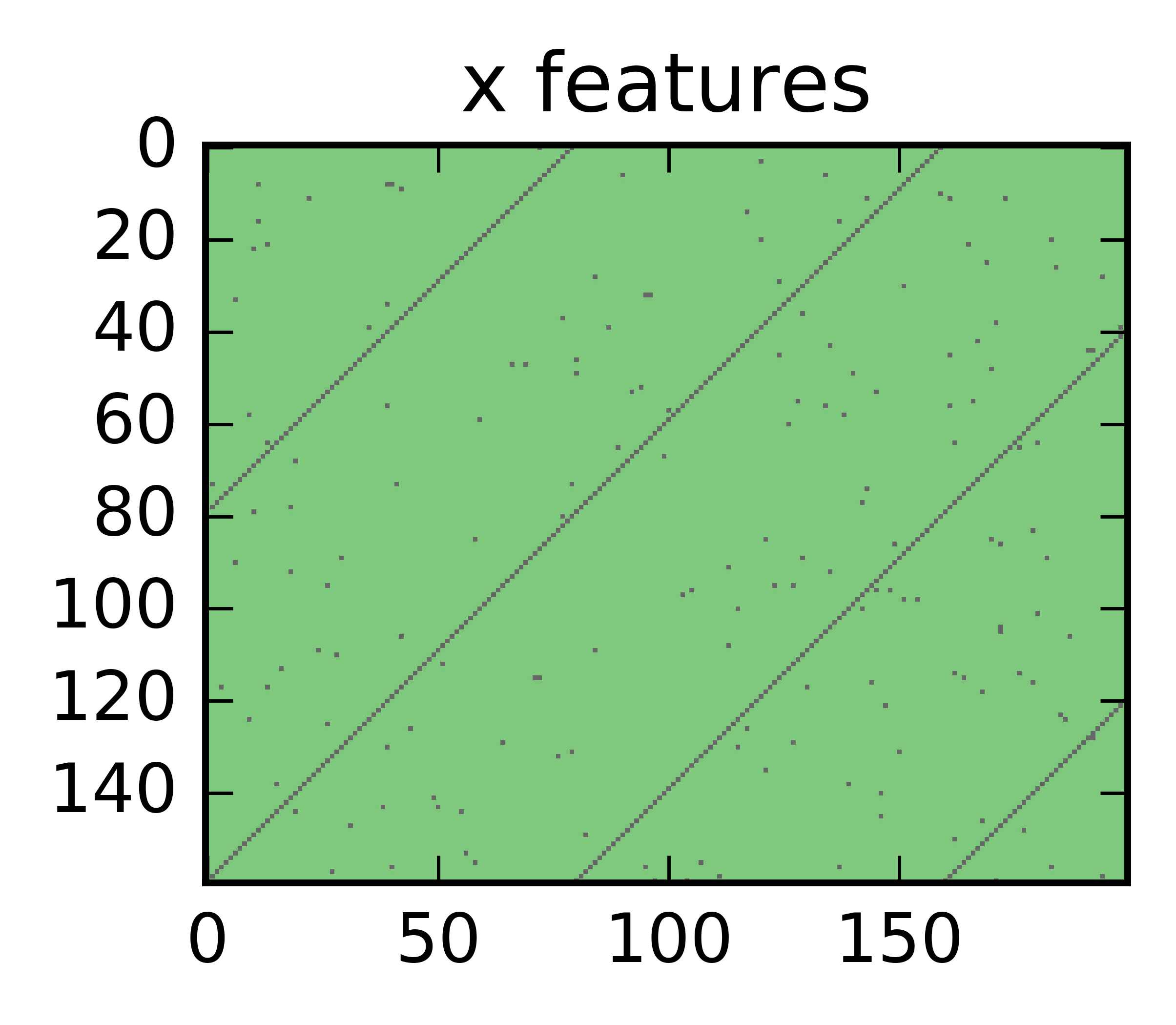
Here the x-axis is time and y the individual sequences. Note how there’s black events sparkled randomly.

Now let’s train an RNN to see what it thinks about it. With a few lines of Keras we can define a small network:

print 'init_alpha: ',init_alpha

np.random.seed(1)
# Store some history
history = History()

# Start building the model
model = Sequential()
model.add(GRU(1, input_shape=(n_timesteps, n_features),return_sequences=True))

model.add(Dense(2))
model.add(Lambda(wtte.output_lambda, arguments={"init_alpha":init_alpha, 
                                               "max_beta_value":4.0}))
loss = wtte.loss(kind='discrete').loss_function

model.compile(loss=loss, optimizer=adam(lr=.01))

model.summary()

init_alpha:  43.4425042957
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
gru_1 (GRU)                  (None, 200, 1)            9         
_________________________________________________________________
dense_1 (Dense)              (None, 200, 2)            4         
_________________________________________________________________
lambda_1 (Lambda)            (None, 200, 2)            0         
=================================================================
Total params: 13.0
Trainable params: 13.0
Non-trainable params: 0.0
_________________________________________________________________

After some epochs it works pretty well. Stacking the predicted Weibull parameters it’s clear that it learned something:

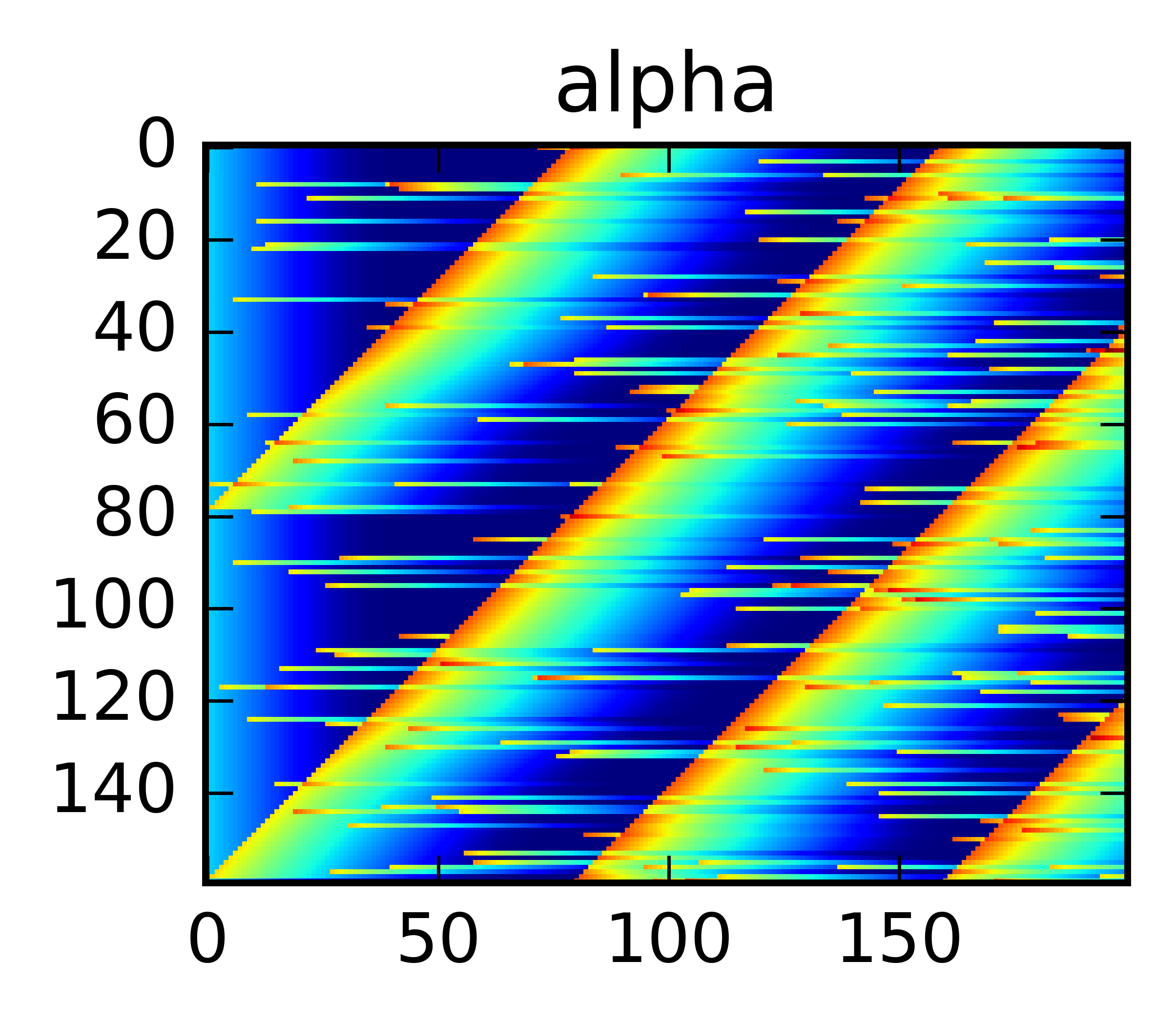
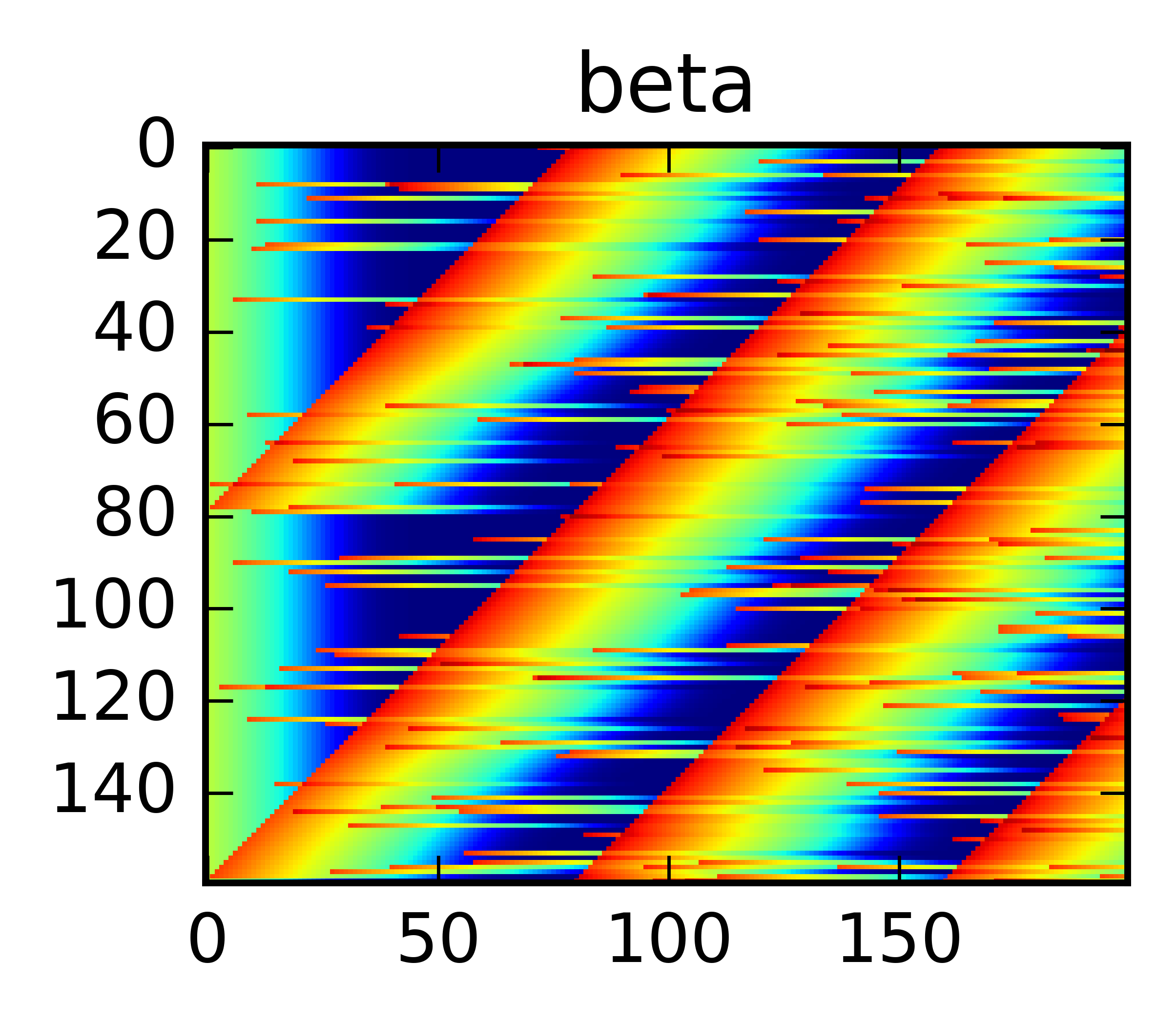
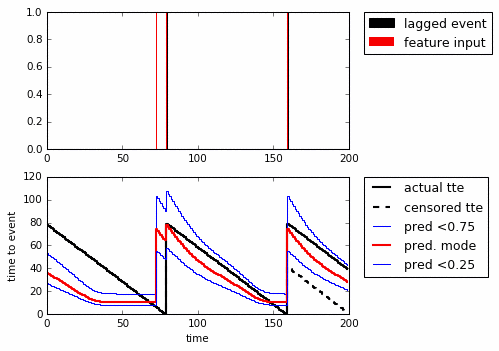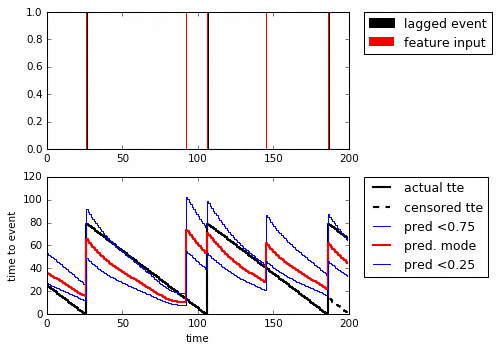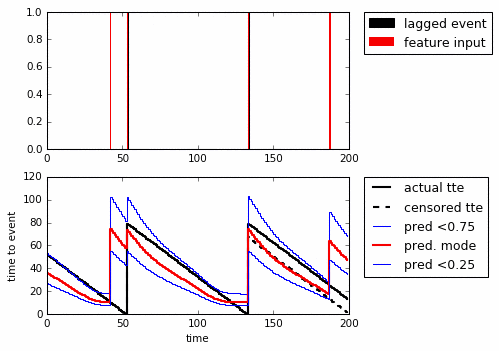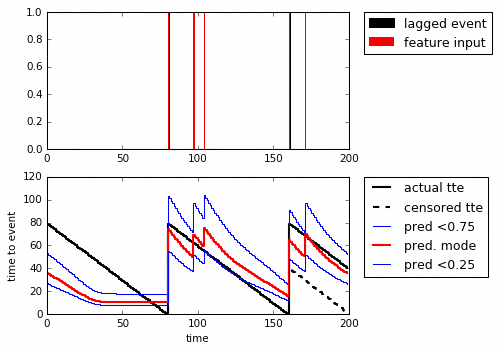
Above we’re looping through the sequences (top to bottom) and show the predicted quantiles. With just one GRU-cell it’s clear that it’s fooled by noise, but it still seems to have learned some type of bayesian reasoning. In particular, even though it was only trained on the censored TTE it manages to predict the actual TTE quite well.

To get the code and improve the results, check out the Github-project and the Jupyter Notebook.

More to come!